【高校・大学数学】覚えると便利な積分問題（tan^3）

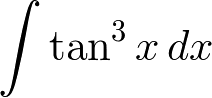
ここでは、積分の問題練習をします。
動画でも解説していますので、よければそちらも見て下さい。

問題
動画解説（YouTube）
解き方
紹介
おわりに＆おすすめ

問題

$\displaystyle\int \tan ^{3}x\,dx$ を求めよう。

動画解説（YouTube）

www.youtube.com

※よければチャンネル登録お願いします。

チャンネルはこちら

解き方

$\displaystyle\int \tan ^{3}x\,dx$ について。

$1+\tan ^{2}x=\dfrac{1}{\cos ^{2}x}$ より、
$\tan ^{2}x=\dfrac{1}{\cos ^{2}x}-1$ であることに注意します。

このとき、

$\begin{aligned}\int \tan ^{3}xdx=\int \tan x\left( \dfrac{1}{\cos ^{2}x}-1\right) dx\\ =\int \dfrac{\tan x}{\cos ^{2}x}dx-\int \tan xdx\end{aligned}$

とできます。

ここで、 $t=\tan x$ とおくと、 $dt=\dfrac{dx}{\cos ^{2}x}$
ですので、
$\begin{aligned}\int \dfrac{\tan x}{\cos ^{2}x}dx&=\int tdt&\\ &=\dfrac{t^{2}}{2}=\dfrac{\tan ^{2}x}{2}&\end{aligned}$
と求まります。

また、
$\begin{aligned}\int \tan xdx=-\int \dfrac{\left( \cos x\right) '}{\cos x}dx\\ =-\log \left| \cos x\right| \end{aligned}$
より、

$\int \tan ^{3}xdx=\dfrac{\tan ^{2}x}{2}+\log \left| \cos x\right|+C$ と求まります。

別のやり方
$\displaystyle\int \tan ^{3}xdx=\int \dfrac{\sin ^{3}x}{\cos ^{3}x}dx$
とするやり方もあります。

この場合、
$\begin{aligned}&\int \tan ^{3}xdx=\int \dfrac{\sin ^{3}x}{\cos ^{3}x}dx&\\ &=\int \dfrac{\left( 1-\cos ^{2}x\right) \sin x}{\cos ^{3}x}dx&\\ &=\int \dfrac{t^{2}-1}{t^{3}}dx&\end{aligned}$
となり、最後の積分より、
$\begin{aligned}\int \dfrac{t^{2}-1}{t^{3}}dt=\log \left| t\right| +\dfrac{1}{2t^{2}}+C\\ =\log \left| \cos x\right| +\dfrac{1}{2\cos ^{2}x}+C\end{aligned}$
と求まります。

もちろんこれでもよいですが、
$1+\tan ^{2}x=\dfrac{1}{\cos ^{2}x}$
と、任意定数Cを使い、
$\int \tan ^{3}xdx=\dfrac{\tan ^{2}x}{2}+\log \left| \cos x\right|+C$
としてもOKです。
※１をCの中にねじ込む手法です。

紹介

noteでメンバーシップをしています。
ドジソンのメンバーシップ｜ドジソン
数学で中心に投稿・活動していますので、よければ参加＆支援してください。

おわりに＆おすすめ

最後に、大学数学のおすすめ参考書まとめの記事を紹介します。
当サイトで人気記事となっていますので、よければ読んでみてください。

≫線形代数（初心者向け）
≫線形代数（上級者向け）
≫集合位相
 ≫複素関数
 ≫微分方程式
 ≫関数解析
 ≫洋書（初心者向け）
≫洋書（上級者向け）
≫LaTeX効率化・おすすめ本

『大学数学記事まとめ』は下から！
dodgson.hatenablog.com

ドジソンの本棚

上の『大学数学』から数学記事検索が簡単にできます

【高校・大学数学】覚えると便利な積分問題（tan^3）

問題

動画解説（YouTube）

解き方

紹介

おわりに＆おすすめ