ドジソンの本棚

上の『大学数学』から数学記事検索が簡単にできます

ドジソンの本棚

本サイトはプロモーションを含みます
トップ > 数学 > 【線形代数】行列の積が定義できるかどうか（どう判断すべきか）

【線形代数】行列の積が定義できるかどうか（どう判断すべきか）

数学 線形代数


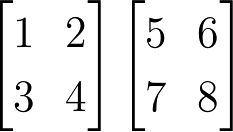
ここでは、線形代数の行列の積について確認します。
動画でも解説していますので、よければそちらも見て下さい。

問：次のA～Dにおいて積が計算できるのはどれか。また、積が計算可能の場合、その値を求めよう。

A=\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}

B=\begin{bmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{bmatrix}

C=\begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix}

D=\begin{bmatrix} 0 & 1 & 2 \end{bmatrix}

動画解説（YouTube）

準備中…

※よければチャンネル登録お願いします。

チャンネルはこちら

解答解説

行列の積が定義できるのは、先の行列をA、後の行列をBとしたときに、
『Aの列の数』＝『Bの行の数』
となるとき、行列の積を計算（定義）できる。

すなわち、
A=\left( l,m\right) ,B=\left( m,n\right)
のように、それぞれ『m』で同じになればよいということ。


上をもとに、A～Dまでを確認してみると、
AB,BA,BC,CD,DC,DAが積の計算ができることがわかる。

次に、それぞれの積の計算を解いていく。
ABのみ丁寧に解き、その他は略解（解のみ）とする。

\begin{aligned}AB&=\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{bmatrix}&\\& =\begin{bmatrix} 1\times 1+2\times 3 & 1\times 2+2\times 2 & 1\times 3+2\times 1 \\ 3\times 1+4\times 3 & 3\times 2+4\times 2 & 3\times 3+4\times 1 \\ 5\times 1+6\times 3 & 5\times 2+6\times 2 & 5\times 3+6\times 1 \end{bmatrix}&\\&=\begin{bmatrix} 7 & 6 & 5 \\ 15 & 14 & 13 \\ 23 & 22 & 21 \end{bmatrix}&\end{aligned}


\begin{aligned}BA&=\begin{bmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{bmatrix}\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}&\\ &=\begin{bmatrix} 22 & 28 \\ 14 & 20 \end{bmatrix}&\end{aligned}

\begin{aligned}BC&=\begin{bmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{bmatrix}\begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix}&\\ &=\begin{bmatrix} -2 \\ 2 \end{bmatrix}&\end{aligned}

\begin{aligned}CD&=\begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix}\begin{bmatrix} 0 & 1 & 2 \end{bmatrix}&\\ &=\begin{bmatrix} 0 & 1 & 2 \\ 0 & 0 & 0 \\ 0 & -1 & -2 \end{bmatrix}&\end{aligned}

\begin{aligned}DC&=\begin{bmatrix} 0 & 1 & 2 \end{bmatrix}\begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix}&\\ &=[ -2] &\end{aligned}

\begin{aligned}DA&=\begin{bmatrix} 0 & 1 & 2 \end{bmatrix}\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}&\\ &=\begin{bmatrix} 13 & 16 \end{bmatrix}&\end{aligned}

以上、今回はここまで。

紹介

大学数学の勉強法を解説しています。期間限定で0円で読めますので、よければ是非。
dodgson.hatenablog.com

おわりに＆おすすめ

最後に、大学数学のおすすめ参考書まとめの記事を紹介します。
当サイトで人気記事となっていますので、よければ読んでみてください。

≫線形代数（初心者向け）
≫線形代数（上級者向け）
≫集合位相
≫複素関数
≫微分方程式
≫関数解析
≫洋書（初心者向け）
≫洋書（上級者向け）
≫LaTeX効率化・おすすめ本

『大学数学記事まとめ』は下から！

Dodgson 読者になる

広告を非表示にする