【すぐ使える】極座標変換でe^(-x^2)ガウス積分について覚えてしまおう【重積分】

※間違い、ご指摘などがあれば（https://twitter.com/Dodgson_007）のDMにご連絡ください。
お問い合わせフォームからもどうぞ（https://dodgson.hatenablog.com/about）

あまりにも有名なので、『できるだけ短く』を意識して進めていきます。
少し雑になりますが、解は出るので問題ないです。
実際に問題を解く時は『はさみうち』を使うなり求められている形に上手く対応してください。

で、問題はこちら。
$\int ^{\infty }_{0}e^{-x^{2}}dx$

ここで、極座標変換を行います。

$x=r\cos \theta ,y=r\sin \theta$
とおきます。

そしてわざと $e^{-\left( x^{2}+y^{2}\right) }$ で考えます。
これは $\int ^{\infty }_{0}e^{-x^{2}}dx$ の2乗なので、あとから外せばいいです。

よって積分は、

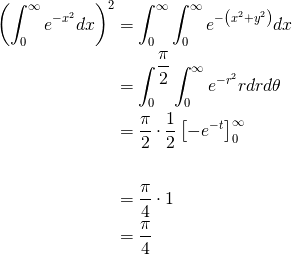
以上より、
$\int ^{\infty }_{0}e^{-x^{2}}dx=\dfrac{\sqrt{\pi }}{2}$

おわり。
簡単ですね。

もっとしっかりしたいなら、領域の内接円と外接円で、はさみうちすればいけます。

ちなみに、 $\int ^{\infty }_{-\infty }e^{-x^{2}}dx=\sqrt{\pi }$ であり、
$e^{-x^{2}}$ のグラフの対称性より上の解の2倍となります。
※グラフは以下の通り。
念のため覚えておきましょう。

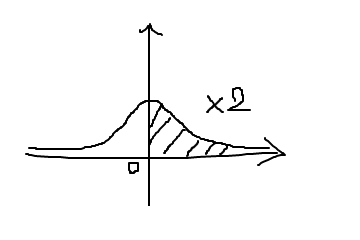
正規分布ですね。

今回はここまでです。
この記事の一番下に関連記事を用意していますので、勉強したい方はそちらからどうぞ。
結構役に立ちます！多分

次記事：より一般的なガウス関数の積分と、その簡単な解き方
$F=\int ^{\infty }_{-\infty }e^{-ax^{2}}dx=\sqrt{\dfrac{x}{a}}$ ←これをやります
dodgson.hatenablog.com

レポート・論文作成に必須となるLaTeXの解説書を出版しました。

初心者向けに解説していますので、よければ是非。

※LaTeXは、高品質な文書を作成するための組版システムです。専門的な論文やレポート、プレゼンテーションなどの作成によく用いられ、美しいレイアウトや数式の表現が特徴です。TeXという組版システムをベースにしており、複雑な文書も簡単に作成できることが利点の一つです。

リンク

✔初心者向け入門書！初めの1冊にもおすすめ！
✔Kindle Unlimitedに対応！
✔綺麗＆美しい文章作成ができる！レポート・論文でも使える！
✔電子書籍だから、いつでも見れる＆使える！

ドジソンの本棚